İki veya Daha Çok Nicel Değişken Arasındaki İlişkiyi Ölçme Metodu: Regresyon Nedir?
Regresyon, bir bağımlı değişken (genellikle Y ile gösterilir) ile diğer bir dizi değişken (bağımsız değişkenler olarak bilinir) arasındaki ilişkinin gücünü ve karakterini belirlemeye çalışan finans, yatırım ve diğer disiplinlerde kullanılan istatistiksel bir yöntemdir. Basit regresyon veya sıradan en küçük kareler (OLS) olarak da adlandırılan doğrusal regresyon, bu tekniğin en yaygın biçimidir. Doğrusal regresyon , en uygun çizgiye dayalı olarak iki değişken arasındaki doğrusal ilişkiyi kurar. Doğrusal regresyon böylece, bir değişkendeki değişikliğin diğerindeki değişikliği nasıl etkilediğini tanımlayan eğime sahip düz bir çizgi kullanılarak grafiksel olarak tasvir edilir.
Bu içeriğimizde regresyon hakkında merak edilen bilgilere ulaşabilirsiniz.
Regresyon Nedir?

Regresyon, bir bağımlı değişken (genellikle Y ile gösterilir) ile diğer bir dizi değişken (bağımsız değişkenler olarak bilinir) arasındaki ilişkinin gücünü ve karakterini belirlemeye çalışan finans, yatırım ve diğer disiplinlerde kullanılan istatistiksel bir yöntemdir. Basit regresyon veya sıradan en küçük kareler (OLS) olarak da adlandırılan doğrusal regresyon, bu tekniğin en yaygın biçimidir. Doğrusal regresyon , en uygun çizgiye dayalı olarak iki değişken arasındaki doğrusal ilişkiyi kurar. Doğrusal regresyon böylece, bir değişkendeki değişikliğin diğerindeki değişikliği nasıl etkilediğini tanımlayan eğime sahip düz bir çizgi kullanılarak grafiksel olarak tasvir edilir.
Doğrusal bir regresyon ilişkisinin y-kesme noktası, diğerinin değeri sıfır olduğunda bir değişkenin değerini temsil eder. Doğrusal olmayan regresyon modelleri de mevcuttur, ancak bunlar çok daha karmaşıktır. Regresyon analizi, verilerde gözlemlenen değişkenler arasındaki ilişkileri ortaya çıkarmak için güçlü bir araçtır, ancak nedenselliği kolayca gösteremez. İşletme, finans ve ekonomide çeşitli bağlamlarda kullanılır. Örneğin, yatırım yöneticilerinin varlıklara değer vermesine ve emtia fiyatları ile bu emtialarla uğraşan işletmelerin hisse senetleri gibi faktörler arasındaki ilişkileri anlamasına yardımcı olmak için kullanılır.
Regresyon hakkında bazı önemli bilgiler:
Regresyon, bağımlı bir değişkeni bir veya daha fazla bağımsız (açıklayıcı) değişkenle ilişkilendiren istatistiksel bir tekniktir.
Bir regresyon modeli, bağımlı değişkende gözlemlenen değişikliklerin açıklayıcı değişkenlerin bir veya daha fazlasındaki değişikliklerle ilişkili olup olmadığını gösterebilir.
Bunu, esas olarak en uygun çizgiyi uydurarak ve verilerin bu çizgi etrafında nasıl dağıldığını görerek yapar.
Regresyon, ekonomistlere ve finansal analistlere varlık değerlemesinden tahmin yapmaya kadar birçok konuda yardımcı olur.
Regresyon sonuçlarının uygun şekilde yorumlanabilmesi için, veriler ve modelin kendisi hakkında çeşitli varsayımların geçerli olması gerekir.
Regresyon, bir veri setinde gözlemlenen değişkenler arasındaki korelasyonu yakalar ve bu korelasyonların istatistiksel olarak anlamlı olup olmadığını ölçer. Daha karmaşık veri ve analizler için doğrusal olmayan regresyon yöntemleri olmasına rağmen, iki temel regresyon türü basit doğrusal regresyon ve çoklu doğrusal regresyondur . Basit doğrusal regresyon, bağımlı değişken Y'nin sonucunu açıklamak veya tahmin etmek için bir bağımsız değişken kullanırken, çoklu doğrusal regresyon sonucu tahmin etmek için iki veya daha fazla bağımsız değişken kullanır.
Regresyon, finans ve yatırım profesyonellerinin yanı sıra diğer işletmelerdeki profesyonellere de yardımcı olabilir. Regresyon, bir şirket için hava durumuna, önceki satışlara, GSYİH büyümesine veya diğer koşul türlerine göre satışları tahmin etmeye de yardımcı olabilir. Sermaye varlığı fiyatlandırma modeli (CAPM), finansta varlıkları fiyatlandırmak ve sermaye maliyetlerini keşfetmek için sıklıkla kullanılan bir regresyon modelidir.
Regresyon ve Ekonometri

Ekonometri , finans ve ekonomideki verileri analiz etmek için kullanılan bir dizi istatistiksel tekniktir. Ekonometri uygulamasının bir örneği, gözlemlenebilir verileri kullanarak gelir etkisini incelemektir. Örneğin bir ekonomist, bir kişi gelirini artırdıkça harcamalarının da artacağını varsayabilir.
Veriler böyle bir ilişkinin var olduğunu gösteriyorsa, gelir ve tüketim arasındaki ilişkinin gücünü ve bu ilişkinin istatistiksel olarak anlamlı olup olmadığını anlamak için bir regresyon analizi yapılabilir.
Analizlerde birkaç açıklayıcı değişken olabileceği unutulmamalıdır. Örneğin, borsa fiyatlarını açıklarken işsizliğe ek olarak GSYİH ve enflasyondaki değişiklikler. Birden fazla açıklayıcı değişken kullanıldığında buna çoklu doğrusal regresyon denir . Bu, ekonometride en yaygın kullanılan araçtır.
Ekonometri bazen, ekonomik teoriye bağlamadan veya nedensel mekanizmalar aramadan, regresyon çıktısının yorumuna çok fazla güvendiği için eleştirilir. Altta yatan süreçlere ilişkin kendi teorinizi geliştirmek anlamına gelse bile, verilerde ortaya çıkan bulguların bir teori ile yeterince açıklanabilmesi çok önemlidir.
Regresyon Hesaplama
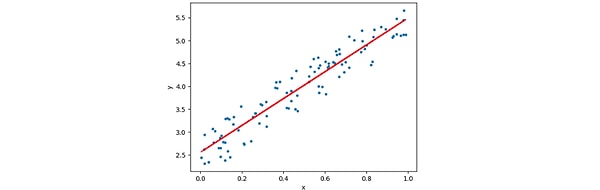
Doğrusal regresyon modelleri, en uygun çizgiyi belirlemek için genellikle en küçük kareler yaklaşımını kullanır. En küçük kareler tekniği, matematiksel bir fonksiyon tarafından oluşturulan kareler toplamının minimize edilmesiyle belirlenir. Buna karşılık, bir veri noktası ile regresyon çizgisi veya veri setinin ortalama değeri arasındaki mesafenin karesi alınarak bir kare belirlenir.
Bu süreç tamamlandıktan sonra (bugün genellikle yazılımla yapılır), bir regresyon modeli oluşturulur. Her tür regresyon modelinin genel biçimi şöyledir:
Basit doğrusal regresyon: Y = A + BX + u
Çoklu doğrusal regresyon: Y = A + B₁ X₁ + B₂ X₂ + B₃ X₃ + ... + Bₜ Xₜ + u
Regresyon Modelleri İçin Tutması Gereken Varsayımlar Nelerdir?
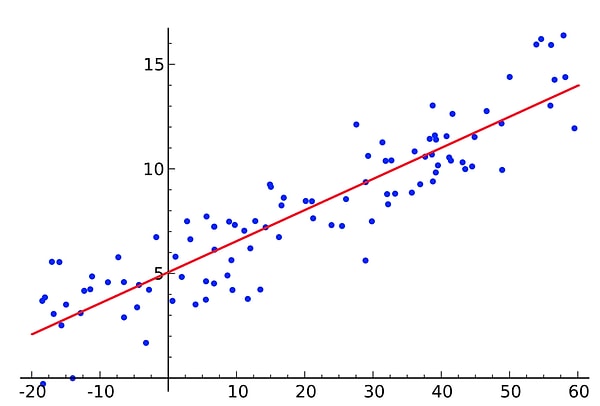
Bir regresyon modelinin çıktısını doğru bir şekilde yorumlamak için, analiz ettiğiniz şeyin altında yatan veri süreciyle ilgili aşağıdaki ana varsayımların geçerli olması gerekir:
Değişkenler arasındaki ilişki doğrusaldır
Homoskedastisite veya değişkenlerin ve hata teriminin varyansının sabit kalması gerektiği
Tüm açıklayıcı değişkenler birbirinden bağımsızdır
Tüm değişkenler normal dağılımlıdır
Keşfet ile ziyaret ettiğin tüm kategorileri tek akışta gör!


Yorum Yazın