Ercan Altuğ Yılmaz Yazio: Oyun Teorisi ile Hayatınızda Doğru Kararlara Yol Açın
“Oyun oynarken ihtiyacımız olan aslında sadece biraz matematik biraz şizofreni.”(John Nash)
Belirsizlik koşullarında karar alma ve karşı tarafın davranışlarının mantığını anlamaya çalışmak tarihin her döneminde insanoğlunun ilgisini çekmiştir. Hepimizin ben böyle yaparsam karşımdaki bunu yapar diyerek fikrimizi rakibimizin yapacağı hamleye göre değiştirdiği zamanlar olmuştur. Farkında olmadan kendimizi pratik bir oyunun içinde buluveririz. Gündelik hayatta birçok yerde karşımıza çıkan ve bir oyuncunun yapacağı hamleyi planlarken diğer oyuncunun alacağı kararları göz önünde bulundurarak karar verdiği bu davranış modeline “oyun teorisi” denir. Oyuncuların kazançları ve kayıpları yalnızca kendi vereceği karara değil rakibinin vereceği karara da bağlıdır.
Oyun teorisi denilince ilk akla gelen isimdir John Nash.
Nobel ödüllü Amerikalı matematikçi John Nash'in hayat hikâyesini anlatan “Akıl Oyunları” filminden hepimizin hafızasında farklı sahneler kalmıştır. Oyun teorisine ilham veren sahne de bunlardan biridir. Arkadaşlarıyla oturduğu bara gelen sarışın kadının tüm dikkatleri üzerine çekmesiyle başlayan sahne de arkadaşının Adam Smith’in “gruptaki herkes kendisi için en iyi olanı yaparsa en iyi sonuca ulaşılacaktır” fikrini savunması üzerine Nash durumun hiç de öyle olmadığını ifade eder. Eğer herkes sarışın kıza asılırsa birbirlerinin önünü keseceklerini bu yüzden de kimsenin sarışını elde edemeyeceğini söyler. Sonrasında sarışının arkadaşlarının ikinci tercih olmayı istemeyeceği için onları reddedeceğini söyler ve Smith’in düşüncesini şu şekilde düzeltir; “en iyi sonuca ulaşmak için bireylerin hem kendisi hem de gruptaki herkes için en iyiyi yapması gereklidir.” İşte John Nash “denge”yi bu şekilde bulur.
Oyun teorisinin varlığı tarihte ilk olarak M.S. 500 yılında Babiller’in toplumsal hayatlarını düzenleyen kuralların yer aldığı Talmud yapıtında rastlanılmıştır. Dönemin yasalarını barındıran Talmud’da evlilik sözleşmeleri de yer alır. Bu sözleşmelere göre üç karısı olan bir adamın ölümü durumunda mirasının dul eşleri arasında nasıl paylaşılacağı tartışılmaktadır. Eğer adamdan eşlerine 100 birimlik bir miras kalırsa eşlerin bu mirası eşit olarak paylaşması, 200 birimlik bir miras kalırsa mirasın 50, 75, 75 oranlarında paylaşılması, eğer 300 birimlik miras kalırsa mirasın 50, 100, 150 oranında paylaşılması önerilmektedir. Teorinin öncüleri 1944 yılında yayınladıkları kitapla matematikçi John von Neumann ve ekonomist Oskar Morgenstern olmasına karşın kuram matematikçi John Nash tarafından geliştirilmiş ve popüler olmuştur. Teori, farkında olmasak da gündelik yaşam ile öylesine iç içe geçmiştir ki ekonomi, ticaret, siyasal bilimler, biyoloji, uluslararası ilişkiler gibi birçok alanda strateji geliştirme ve karar verme aşamalarında kullanılmaktadır.
İmkânsız diye bir şey yoktur. Sadece bazı şeylerin olma olasılığı biraz daha düşüktür. (Adam Fawer)
Oyun teorisinin temelinde “bir oyuncunun kaybı diğerinin kazancıdır” (sıfır toplamlı oyunlar) ilkesi yer alırken, daha sonradan farklı oyunları-modelleri çözümleyerek geniş bir alana yayılmıştır.
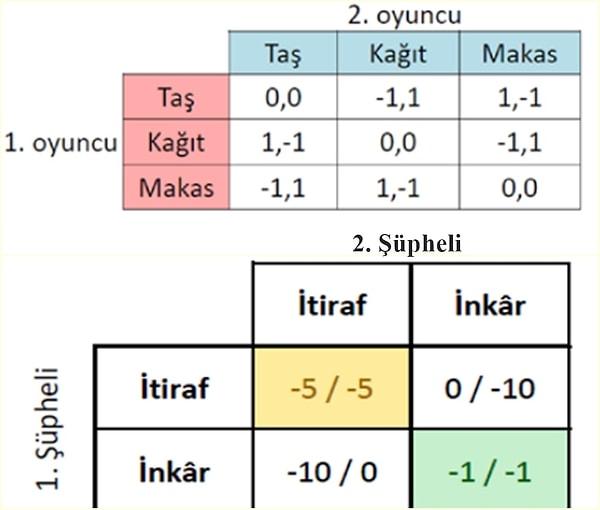
Sıfır toplamlı oyunlara örnek olarak dama, satranç, kart oyunları gibi oyunlar gösterilebilir. Hepimizin bildiği taş-kâğıt-makas oyununda acaba oyun teorisi kullanarak kazanan hep biz olabilir miyiz? Bunun üzerine yazılmış 200 sayfalık bir rehber olduğunu biliyor musunuz?
Gelelim oyun teorisinin “mahkûm ikilemi (prisoner’s dilemma)” ve “kadın-erkek savaşı (battle of the sexes)” örneklerine bunlar oyun teorisinde Nash dengesini anlatan en popüler örneklerdir.
John F. Nash’in literatüre kazandırdığı, özünde “herkes için en iyi strateji” olarak değerlendirebileceğimiz “Nash Dengesi”, oyun teorisinin temelini oluşturur.
İki şüpheli bir suçtan dolayı polis tarafından yakalanıp ayrı odalarda sorgulanmaya başlanır. Böylece ikisi de diğer arkadaşının sorgulamasının nasıl gittiği hakkında bilgiye sahip değildir. Buradaki varsayım, şüphelilerin gerçekten suçu işledikleridir. Sorguda suçu itiraf etme ya da reddetme olmak üzere sadece iki seçenekleri bulunmaktadır. Eğer şüphelilerin ikisi de suçu işlediklerini reddederlerse, polis ikisini de büyük suçtan dolayı mahkûm edemeyecek; fakat yine de başka bir küçük suçtan dolayı ikisi de birer yıl cezalandıracaktır. Eğer biri inkâr eder, diğeri itiraf ederse, reddeden şüpheli 10 yıl ceza alacak; itiraf eden ise ceza almayacaktır. Eğer ikisi de itiraf ederlerse 5’er yıl ceza alacaklardır.
Eğer şüphelilerin önceden anlaşma şansı olsaydı ikisi de inkâr etmeyi seçerdi. İşte bu oyunun Nash dengesidir. Yani herkesin oyundan en karlı çıkarımı yaptığı yer, denge noktası. Ancak karar verme aşamasında ya o itiraf ederse düşüncesi bireyleri bu denge noktasından uzaklaştırır ve ikisi de en mantıklı olanın itiraf etmek olduğunu düşünür. Hâlbuki ikisi de inkâr etseydi 1’er yıl ile bu işten kurtulacaklardı.
Peki, şimdi bir düşünelim; İstanbul’da yaşıyorsunuz ve hiç tanımadığınız biriyle Cumartesi günü buluşacaksınız yer ve saat belli değil. Sadece üzerinde taşıyacağı bir nesneyi biliyorsunuz ve tabii bu kırmızı bir karanfil ☺ Buluşma için aklınıza gelen ilk nokta neresi olur? Bu soruya çoğunluğun vereceği cevap büyük olasılıkla Taksim Meydanı olacaktır. Çünkü Taksim Meydanı, böyle bir durumda İstanbul’da yaşayanlar için akla gelen ilk yerdir. İşte oyun teorisinde insanların akıllarına özel ya da doğal olması sebebiyle ilk sırada gelen akılcı tercihe “Schelling noktası” denir. Korkak tavuk örneği de “Schelling noktası” için verilebilecek en meşhur örneklerdendir.
Farkında olmasak da oyun teorisi hayatımızın birçok noktasında karar verme stratejilerimiz etkileyen bir modeldir. Telefon aniden kesilince bile anlık olarak oyun teorisinden yararlanırız. Sadece bireysel boyutta değil uluslararası ilişkilerde dahi insanların kaderini belirleyebilir. Rekabetçi bir yaklaşım mı seçmeli yoksa işbirliği mi?
Riske karşı yaklaşımlarımız belki de hayatımızın kırılma noktasını oluşturacaktır kim bilir…
Bu yazı Gamfed Türkiye gönüllülerinden Zeynep Aydın’ın katkılarıyla yazılmıştır.
Yorum Yazın