Birçok İnsan Bilmese de Siz Bilin: Aralarında Sıkı Sıkıya İlişki Olan Matematik ve Müzik
Matematik dünyada pek çok öğrenci için en sıkıntılı derslerden birisidir. Müzik, özellikle okul öncesi eğitiminde, matematik eğitiminde yeni bir yaklaşım alarak kullanılabilir. Bunların yanında, müzik yeteneği ve matematik yeteneği arasındaki ilişki eğitime yeni boyutlar katabilir.
Bu iki disiplin antik devirlerden itibaren karşılaştırılmış ve ilişkilendirilmiştir. Her ikisinde de hem estetik hem evrensel bir dil hem de bir stil vardır. Bir müzisyen Bach'ı nasıl ilk melodilerinden anlayabiliyorsa, bir matematikçi de Gauss'u ilk satırlardan fark edebilir.
Müziğin kökenindeki matematik
Matematik ve müzik ilişkisi çeşitli boyutlarda düşünülebilir. Müziğin kökenindeki matematik gibi. Müziğin armonik yapısı matematikseldir. Sadece matematikseldir demek yanlıştır ancak belirli kurallara bağlı olarak biçimlendirilir. Tarihin değişik dönemlerinde değişik kurallar uygulanmıştır ancak mutlaka matematiksel bir köken olmuştur.
Müziğin bilişsel aktiviteler üzerindeki etkisi
Gerek arka plan müziği olarak kullanılan müzik, gerekse müzik eğitimi, kişilerin bilişsel performanslarını, dolayısı ile matematik performanslarını geliştirmektedir. Müzik pek çok insan için bir 'eğlence kaynağı' , matematik ise pek çok insan için bir 'baş belası' iken, müziğin matematik eğitimi üzerindeki olumlu etkilerini kullanmak oldukça akılcı bir davranış olacaktır.
Müziğin nörolojik çalışmalarla ilgisi
Son yıllarda teknolojinin de hız kazanması ile birlikte insan beyni çeşitli tekniklerle incelenir duruma gelmiştir. Müziğin insan beyni üzerindeki etkisi bu teknikler sayesinde çok daha açık bir şekilde görülmektedir. Bir diğer boyut ise yetenek ilişkisi ile ilgilidir. Matematik yeteneği ve müzik yeteneği arasında bulunacak bir ilişki eğitime büyük yenilikler getirebilir.
Müziğin temelindeki matematik
Müzik ve matematik arasındaki ilişkinin incelenmesi eski Yunanlılara kadar uzanır. Eski Yunan' da müzik, matematiğin 4 ana dalından biri olarak kabul edilmiştir.
Pisagor okulunun programına göre müzik; Aritmetik, Geometri ve Astronomi ile aynı düzeyde kabul görmüştür. Bir telin değişik boyları ile değişik sesler elde edildiğini ortaya çıkartan Pisagor, M.Ö. 6. yüzyılda yaşamıştır ve bugün kullanılmakta olan müzikal dizinin temelini oluşturması açısından oldukça önemli bir iş yapmıştır.
Pisagor ve müzik
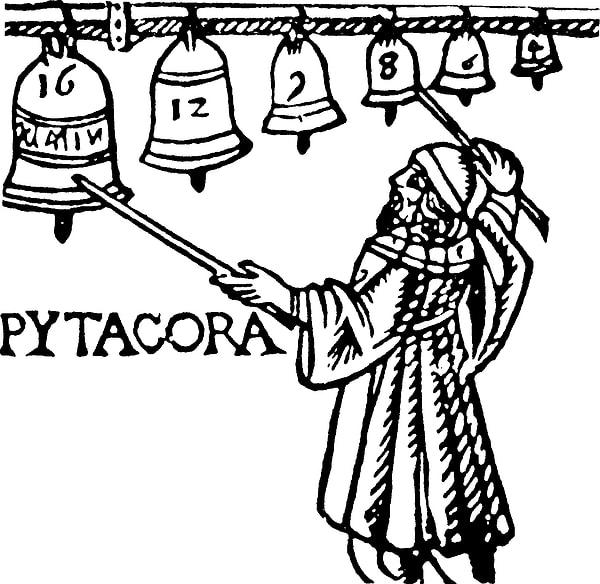
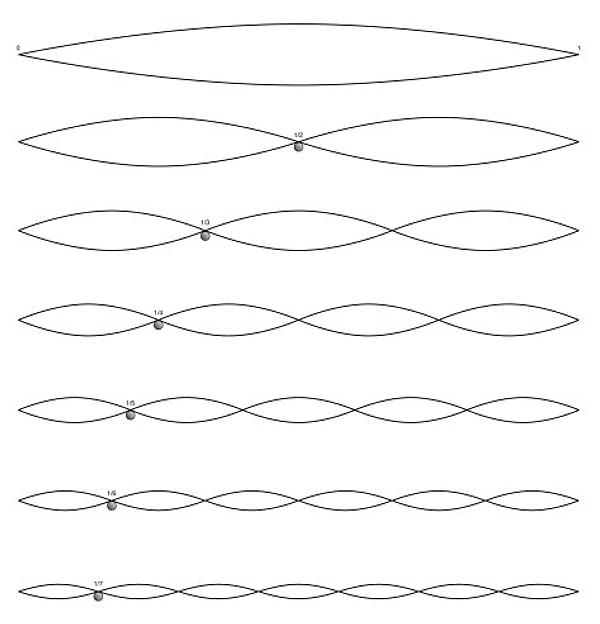
Pisagor, 12 birimlik bir teli ikiye bölmüş ve oktavı elde etmiştir. Elde edilen 6 birimlik uzunluk (telin yarısı), 12 birimlik uzunluğun bir oktav tizidir. Pisagor 8 birimlik uzunluk ile (telin 2/3 ü) 5’li aralığı, 9 birimlik uzunluk ile (telin ¾ ü) 4’lü aralığı bulmuştur.
Antik devirde dört sesin bir arada duyulması prensibi 'tetrakord' olarak adlandırılmakta ve müzik teorisinin temel kuralı olarak sayılmaktadır. Böylelikle tetrakord, 6, 8, 9 ve 12 ile elde edilmiştir.
Pisagor, telin 8/9 u ile 1 tam tonu elde etmiştir, ancak bir notaya 6 kez tam ton ilave edildiğinde neredeyse o notanın oktavı elde edilmiştir ki bu da 'Pisagor koması' olarak adlandırılır. Bu durumda Pisagor sisteminde bazı değişikliklere gerek duyulmuş ve böylece zaman içinde tampere edilmiş bir şekilde 12 eşit yarım tonluk bir sistem geliştirilmiştir. 1 tam ton 8/9 ile değil iki yarım ton ile gösterilmiştir.
Kısacası Pisagor, evrendeki ve müzikteki matematiği keşfedenlerdendir.
Tavşan Çiftliği ve Altın Oran
Estetik anlayışındaki en eski ve en yerleşik kavram, kökü Sokrates ve öncesi filozoflara uzanan oransal uyumluluk, oran ve sayı kavramlarıdır. Yunan düşüncesinde 'oran' anlayışı büyük önem taşımaktadır.
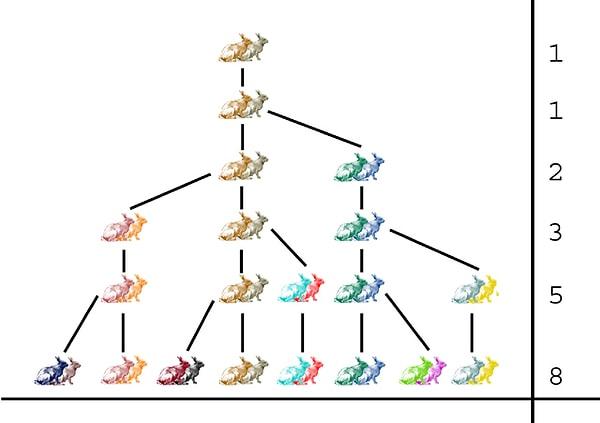
Leonardo Fibonacci (1175-1240) bir İtalyan matematikçisidir. Matematik biliminde önemli çalışmaları olmuştur. Ancak en çok 'tavşan çiftliği' problemi ile meşhur olmuştur. Probleme göre; bir çift tavşan var ve bir ay geçtikten sonra her yeni çift tavşan bir çift tavşan doğuruyor. Her yeni doğan çift ikinci ay birer çift tavşan doğurur ve bu böylece devam eder. Kaç ay sonra kaç çift tavşan olur. Sonuçta karşımıza şu şekilde bir seri çıkar;
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987...
Seriye bakacak olursak, son iki sayının toplamı bize bir sonraki sayıyı vermektedir. Burada bizim için önemli olan orandır. Dikkat edilecek olursa iki ardışık sayının oranı (küçük sayının büyük sayıya oranı) aynı sayıya yakınsamaktadır. 0, 61803398......Bu oran resimde, mimaride ve müzikte çeşitli dönemlerde 'altın oran' veya 'mükemmel oran' olarak kullanılmıştır.
Peki bunlar nerelerde kullanıldı?
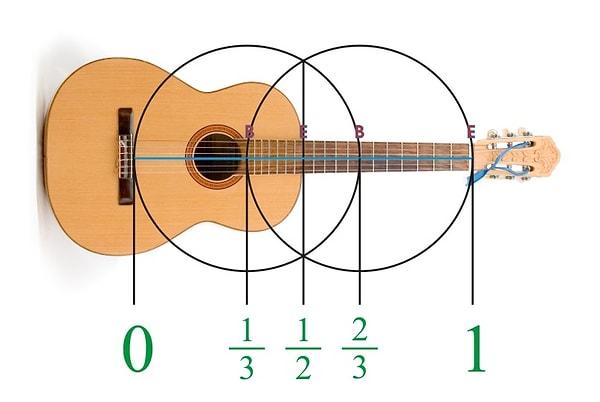
Bella Bartok, altın oranı kullanan bestecilerdendir. Bartok, Fibonnacci sayıları ile bir dizi oluşturmuş ve bu dizinin elemanlarını bestelerinde kullanmıştır 'Music for strings, percussion and celeste' parçasının ilk bölümünde, 89 ölçünün 55. ölçüsünde kullanılmıştır
Bu konuda yaygın olarak bilinen bir parça Haendel'in 'Hallelujah' eseridir. Bu eserde toplam 94 ölçü vardır. En önemli kısımlardan birisi; solo trompetlerin girişi 'Kings of kings', 57. ve 58. ölçülerde başlamaktadır. Yani 94 ölçünün 8/13’inde.
Mozart'ında altın oranı kullanıp kullanmadığına dair çeşitli görüşler vardır. John F.Putz'a göre Mozart'ın eserleri bir dahi işidir ve sayılarla oynamayı seven birisinin işidir. O'na göre Mozart altın oranı biliyordu ve eserlerinde kullanmıştır
Müziğin matematik eğitimine katkısı
Matematik pek çok ülkede eğitim açısından en sıkıntılı derstir ve sonuç olarak şu konuda hemen herkes birleşmektedir ki; matematik eğitiminde yeni yaklaşımlara ihtiyaç vardır.
Okul öncesi dönem, çocukların yeteneklerini ortaya çıkartmak ve yönlendirmek açısından büyük önem taşımaktadır. Matematiğin ve müziğin temeli bu dönemde atılmalıdır.
Müzik ile bilişsel aktivitelerin gelişimi konusunda yıllardır çeşitli araştırmalar yapılmıştır. Ancak medya tarafından en çok ilgi gören araştırma 1993'te 'Mozart Etkisi' (Mozart Effect) olarak duyurulmuş ve çok dikkat çekmiştir. Ki bu konuyu daha önce burada paylaşmıştık.
Müzik ruhun gizli bir matematiksel problemidir
19. yy. da J. Fourier, müzikal serinin niteliğini incelemiştir. Fourier, müzik aleti ve insandan çıkan bütün müzikal seslerin matematiksel ifadeler ile tanımlanabileceğini ve bununda periyodik sinüs fonksiyonları ile olabileceğini ispatlamıştır. Ünlü Matematikçi Leibniz, 'Müzik ruhun gizli bir matematiksel problemidir' demiştir.
Matematik ve müzik pek çok açıdan birbiri ile ilişkili iki disiplindir. Antik çağlardan itibaren bu ilişki fark edilmiş ve pek çok matematikçinin ve düşünürün ilgisini çekmiştir. Bilimin ve sanatın temsilcileri sayılan bu iki disiplinin birbiri ile olan ilişkisinin etkin kullanımı günümüzde pek çok açıdan olumlu sonuçlar doğurabilir.
Keşfet ile ziyaret ettiğin tüm kategorileri tek akışta gör!
Test
Gündem
Magazin
Video
Yorum Yazın
Matematik dediğin labne peyniri gibidir. Her şeyle gider. Hiç sırıtmaz...
Ritim başlı başına bir matematiktir.
Müzik hayattır zaten boşa demiyoruz https://bit.ly/2qTU6nr